Given the heads to two sorted linked lists, return a pointer to the head of a linked list containing all elements in both lists in sorted order.

While this problem seems/is fairly straight forward, there are a few implementation and complexity differences we can look at when dealing with contiguous arrays vs linked lists.

Merging 2 Sorted Arrays

Let’s look at a simpler version of the same problem. When faced with two sorted arrays, most people jump to the merge() subroutine in classic mergeSort() to merge them together in $O(n+m)$ time and $O(n+m)$ space, where $n$ and $m$ are the number of elements in each input array.

Merging two sorted arrays has a simple enough implementation, due to the fact that we need space asymptotically linear to the total number of elements. Our space requirement gives us the tradeoff of easy implementation because we never modify the input arrays. Instead, we just follow the colloquially named “two finger algorithm” (not Floyd’s cycle detection), iterating through both input arrays and copying the smaller of the two values we’re assessing into our final array. We then continue in the array we took the value from and repeat. The input array that has values left over once we exhaust the other gets its remaining elements copied one-by-one to the final list.

Merging 2 Sorted Linked Lists

Merging two sorted linked lists differs in implementation and complexity. For one, we can merge two sorted linked lists in $O(1)$ space. This is because we’re working with pointers as opposed to elements in contiguous memory. We don’t have to actually copy and package up each value we see in each list when we come across it. Instead, we just evaluate each element (linear time complexity) and change pointers around in-place if need be. Let’s take a closer look at how we’d do this.

// Sample list node
struct Node {
  int data;
  Node* next;
  Node(int data, Node* next = NULL) : data(data), next(next) { }
};

To merge two sorted linked lists, we need to maintain pointers to the current list nodes we’re looking at in each input list. Then we can use these current pointers, aCurr and bCurr for example, to traverse through each list. We want to choose the smaller of the two to focus on. Either aCur->data <= bCurr->data or bCurr->data < aCurr->data will be our first conditional we run into while we’re able to traverse the lists. In this example, the former is true and we need to figure out what should come after aCurr.

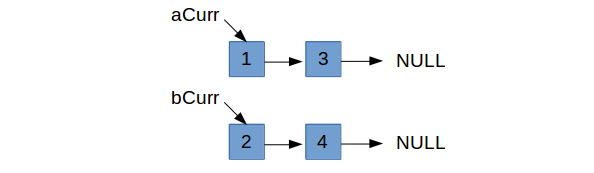
The next two smallest nodes to pick from are aCurr->next and bCurr. As it stands, aCurr’s next is pointing to aCurr->next (the next node in $a$’s list). So it makes sense that we would only set aCurr->next = bCurr if bCurr is strictly less than what aCurr already points to. Since bCurr->data < aCurr->next->data, we set aCurr->next = bCurr.

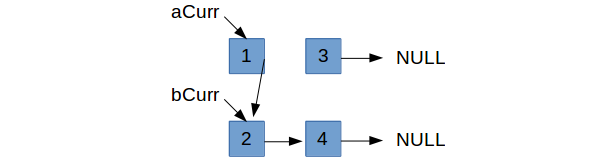
Note how we’ve lost contact with the rest of the top list. Since this is not a contiguous array, we can’t just index forward to increment aCurr. Instead, we need to keep some pointer to the next node in the event we set aCurr->next to bCurr. Then we can set our aCurr equal to the pointer we kept to increment our current node.

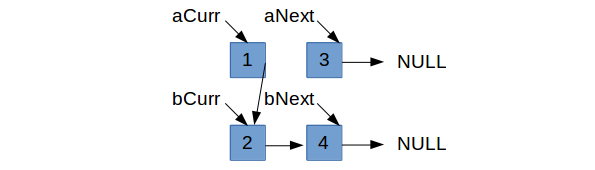
Let’s go back and consider the case in which bCurr->data < aCurr->data. Of course, the next two smallest nodes are bCurr->next and aCurr. So we need to figure out which one should come after bCurr. As it stands, bCurr’s next is obviously pointing to bCurr->next (the next node in $b$’s list).

You might think we should only set bCurr->next = aCurr if aCurr->data is strictly less than bCurr->next->data, otherwise, we shouldn’t bother. However, that actually leads to an insidious bug. Let’s move forward with this logic to see why it is wrong.

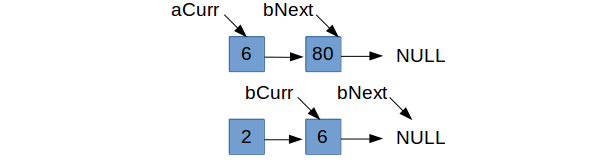
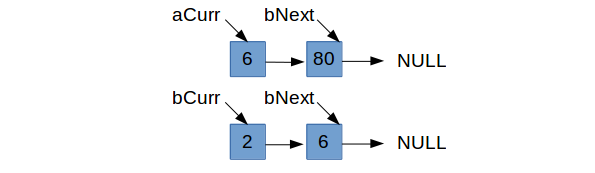
We’ve incremented bCurr and are at the case where aCurr->data <= bCurr->data, so we are focusing on aCurr and figuring out what comes next. As with our logic earlier, we’ll only set aCurr->next = bCurr if bCurr makes a compelling enough case (namely it is strictly less than the current aCurr->next). Since 6 < 80, we set aCurr->next = bCurr and increment aCurr.

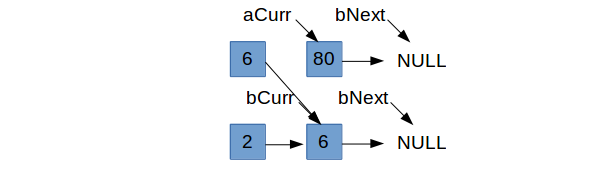
Therein lies the problem. Nothing was ever pointing to the old aCurr and it was not designated to be the head of the entire list. So it is lost in memory limbo, only to become a leak. Instead, something needs to give. If we decide to be selfish when focusing on aCurr, in that we only set aCurr->next = bCurr if bCurr->data < aCurr->next->data, then we need to be more lenient when focusing on bCurr. If the value in aCurr $\leq$ bCurr->next, we need to set bCurr->next = aCurr so that the logic is handled properly in the next iteration.

See the code below for the full implementation of this algorithm:

Here’s a link to Leetcode’s Merge Two Sorted Lists OJ problem.